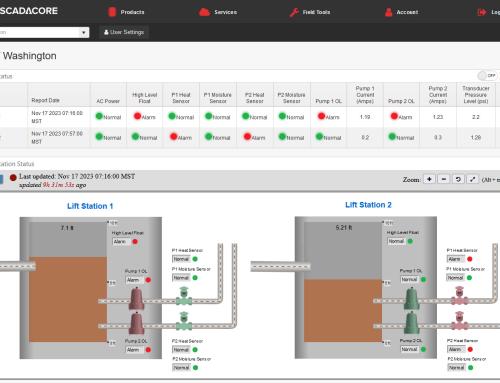
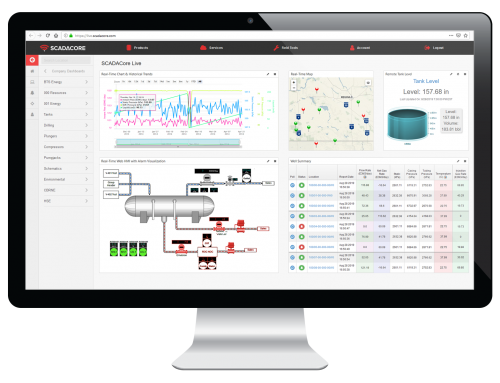
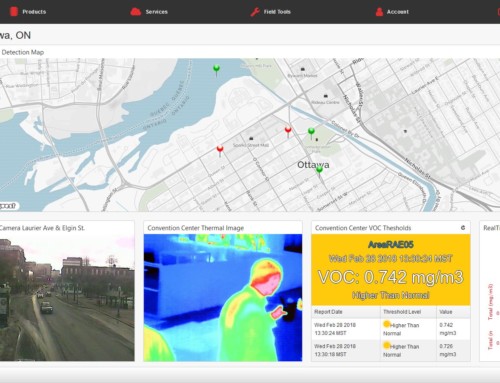
When dealing with fluctuating data rolling averages are needed to even out the highs and the lows. For example a methane detector could bounce between 9% and 11% LEL with very little change in the actual methane in the air. An alarm set at 10% would constantly be alarming and then clearing causing operators or residents to lose faith in the system or simply turn it off to avoid the messages.

Rolling Averages

Rolling averages are also called moving averages or time weighted averages. A lot of information can be found in the Wikipedia page: https://en.wikipedia.org/wiki/Moving_average, but unless you are familiar with math terminology you may have some difficulty understanding the formulas.

In this blog we will talk about Cumulative Moving Average which generally works for most scenarios as it puts more emphasis on the newer values as the previous ones fall off.

Cumulative Moving Average

The cumulative moving average means that every value inside the window will be treated equally. If you are taking a sample every 10 seconds and produce a 1 minute average from them.

10 11 9 11 10 9 10 9 10 11 8 11 10 11

With this sample the latest values are underlined giving us a REAL average of (10+11+9+11+10+9+10+9+10+11) / 10 = 10. If you have the programming functions available and would like to keep a buffer, averaging is a viable method but it can be complicated as you have to deal with circular buffers and is even more difficult when you are dealing with Weight Moving Averages.

Using the formula provided to us by wikipedia.

\textit{CMA}_{n+1} = {x_{n+1} + n \cdot \textit{CMA}_n \over {n+1}} = {\textit{CMA}_n} + {{x_{n+1} - \textit{CMA}_n} \over {n+1}}

In practice the formula would look like this:

CMA1 = 0 + (11 – 0)/ 1 = 11 (this makes sense, we have one value the average should be that value)

CMA2 = 11 + (10-11)/ 2 = 10.5 (again this makes sense as the average of 11 and 10 is 10.5)

CMA3 = 10.5 + (11-10.5)/2 = 10.67  (Actual Average of last 10 values= 10.67)

CMA4 = 10.67 + (8-10.75)/2 = 10 (Actual Average of last 10 values= 10)

CMA5 = 10.2 (Actual Average of last 10 values= 10.2)

CMA6 = 10.167 (Actual Average of last 10 values= 10.167)

CMA7 = 10 (Actual Average of last 10 values= 10)

CMA8 = 10 (Actual Average of last 10 values= 10)

CMA9 = 9.89 (Actual Average of last 10 values= 9.89)

CMA10 = 9.9 (Actual Average of last 10 values= 9.9)

CMA11 = 10 (Actual Average of last 10 values= 9.9) Here we begin to deviate

CMA12 = 9.9167 (Actual Average of last 10 values= 9.8)

CMA13 = 10 (Actual Average of last 10 values= 9.8)

CMA14 = 10 (Actual Average of last 10 values= 10) Values are the same out of coincidence

Although the rolling averages are not exact they are really quite close to the actual averages this allows the programmer to implement an averaging without having to save hundreds of items in an array or implement a circular queue.

Post Views: 2,155